Nichtlineare Regression
In naturwissenschaftlich- technischen Anwendungen stellt sich oft das Problem, die Beziehungen von zwei Variablen in optimaler Weise zu beschreiben. Wird ein nicht -linearer Zusammenhang vermutet, stehen mehre Verfahren zur Verfügung. Ein Verfahren ist die Annäherung der Funktion durch ein Polynom \(y=a\cdot x^2 + b\cdot x +c\). Mit dem Verfahren lassen sich zwar die Messpunkte gut anpassen, es besteht aber immer die Gefahr, dass die Messpunkte zwar auf der Kurve liegen aber die Kurve nicht den naturwissenschaftlichen Zusammenhang beschreibt. Ist die grundlegende Kenntnis über die zugrunde liegenden Zusammenhänge vorhanden, ist es oft möglich nicht lineare Ausgangsprobleme auf lineare zurückzuführen. Dabei müssen die Parameter der Funktion in linearer Form dargestellt werden. Zum Beispiel die Entladung eines Kondensators \(u_t = u_0 \cdot \exp(\frac{t}{R \cdot C})\) lässt sich in die Form \(\ln{u}= \ln{u_0} - \frac{t}{R \cdot C}\) bringen.
#-- Gemessene Werte Entladung eines Kondensators
#-- u = Spannung, t = Zeit, u0=Anfangsspannung, R = Widerstand, C = Kapazität
#-- u(t) = u0*exp(-t/R*C)
#-- ln(u) = ln(u0) - t/R*C
t <- c(1, 4, 7, 10, 15)
u <- c(80, 45, 25, 14, 5)
y <- log(u)
#-- lineare Regression
dat <- data.frame(t, u, y)
fit <- lm(y ~ t, dat)
#-- Rücktransformation der Parameter
# u0 = Anfangsspannung, R = Widerstand, C= Kapazität
round(c(u0 = exp(coef(fit)[1]), RC = (-1 / coef(fit)[2])), 2)## u0.(Intercept) RC.t
## 98.98 5.06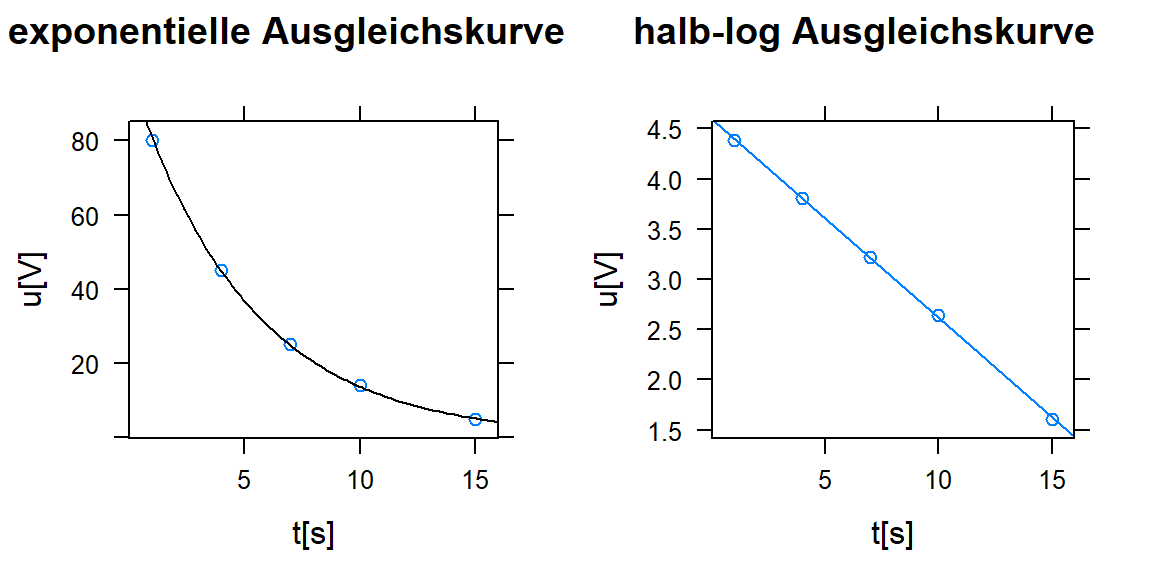
Figure 1: Entladung eines Kondensators
In Fällen, in denen keine Linearisierung existiert oder wenn durch die Linearisierung die Voraussetzungen der Regressionsrechnung verletzt werden, kann durch geeigneter Iterationsverfahren schrittweise eine Lösung bestimmt werden.
Literatur
Papula, L., Mathematik für Ingenieure und Naturwissenschaftler Band3, 3 Auflage, Viewegs, 1999
